Los signos de agrupacion sirven para agrupar o separar distintas operaciones. Los signos de agrupacion conocidos son:
* Parentesis ( )
* Llaves { }
* Corchete [ ]
* Raya --
Los signos de agrupacion se resuelven de adentro hacia afuera, es decir, del interior al exterior.
Reglas:
1- Si delante del signo de agrupacion hay un signo mas (+) todo lo que esta adentro se queda igual.
2- Si delante del signo de agrupacion hay un signo menos (-) toda la exprecion que esta adentro cambia de signo.
3- Si delante del signo de agrupacion hay un numero toda la exprecion que esta adentro se multiplica por ese numero.
Buscar este blog
jueves, 30 de enero de 2014
La aritmetica
La aritmética, es la rama de la matemática cuyo objeto de estudio son los números y las operaciones elementales hechas con ellos: suma, resta, multiplicación y división.
Al igual que en otras áreas de la matemática, como el álgebra o la geometría, el sentido de «la aritmética» ha ido evolucionando con el progresivo desarrollo de las ciencias. Originalmente, la aritmética se desarrolla de manera formal en la Antigua Grecia, con el refinamiento del rigor matemático y las demostraciones, y su extensión a las distintas disciplinas de las «ciencias naturales».[] En la actualidad, puede referirse a la aritmética elemental, enfocada a la enseñanza de la matemática básica; también al conjunto que reúne el cálculo aritmético y las operaciones matemáticas, específicamente, las cuatro operaciones básicas aplicadas ya sea a números (naturales, fracciones, etc.) como a entidades matemáticas más abstractas (matrices, operadores, etc); también a la así llamada alta aritmética,[3] mejor conocida como teoría de números.
El algebra
El álgebra,
es la rama de la matemática que estudia la combinación de elementos de
estructuras abstractas acorde a ciertas reglas. Originalmente esos elementos
podían ser interpretados como números o cantidades, por lo que el álgebra en
cierto modo originalmente fue una generalización y extensión de la aritmética.
En el álgebra moderna existen áreas del álgebra que en modo alguno pueden
considerarse extensiones de la aritmética (álgebra abstracta, álgebra
homológica, álgebra exterior, etc.).
Valor numerico
El valor numerico de una expresion algebraica se obtiene al sustituir todas sus variables x, y, z, ... por numeros.
Cuadrilatero
Un cuadrilatero es la union de segmentos formados con cuatro puntos no colineales y coplanares, te tal modo que dichos segmentos solo se intersecten en sus ectremos.
Triangulos
Un triangulo es una figura que se forma al trazar los segmentos comprendidos entre los puntos A, B y C no alineados. Estos segmentos son los lados del triangulo y los puntos A, B y C sus vertices.
Las alturas de un triangulo son los segmentos perpendiculares que se van de un lado o su prolongacion al vertice opuesto.
Las alturas de un triangulo son los segmentos perpendiculares que se van de un lado o su prolongacion al vertice opuesto.
Ecuaciones trigonometricas
Las ecuaciones trigonometricas son igualdades en que hay presentes funciones trigonometricas de angulos desconocidos.
Las ecuaciones trigonometricas son satisfechas por un conjunto infinito de valores de x.
Las ecuaciones trigonometricas son satisfechas por un conjunto infinito de valores de x.
miércoles, 29 de enero de 2014
Cono (Geometria)
En geometría, un cono recto es un sólido de revolución
generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos.
Al círculo conformado por el otro cateto se denomina base y al punto donde
confluyen las generatrices se llama vértice.
Superficie cónica se denomina a toda superficie reglada conformada por el conjunto de rectas que teniendo un punto común (el vértice), intersecan a una circunferencia no coplanaria.
Superficie cónica se denomina a toda superficie reglada conformada por el conjunto de rectas que teniendo un punto común (el vértice), intersecan a una circunferencia no coplanaria.
Toro (Geometria)
En geometría, un toro
o torus es una superficie de revolución generada por una circunferencia
que gira alrededor de una recta exterior coplanaria (en su plano y que no la
corta). La palabra «toro» proviene del vocablo en latín torus, el cual
en castellano significa «bocel» o «murecillo», que es una moldura redondeada de
la basa, con forma de hogaza de pan. Muchos
objetos cotidianos tienen forma de toro: un dónut, una rosquilla, la cámara de
un neumático, etc.
Cilindro
En geometría, un cilindro es una superficie de las denominadas cuádricas formada por el desplazamiento paralelo de una recta llamada generatriz a lo largo de una curva plana, que puede ser cerrada o abierta, denominada directriz del cilindro.
Si la directriz es un círculo y la generatriz es perpendicular a él, entonces la superficie obtenida, llamada cilindro circular recto, será de revolución y tendrá por lo tanto todos sus puntos situados a una distancia fija de una línea recta, el eje del cilindro. El sólido encerrado por esta superficie y por dos planos perpendiculares al eje también es llamado cilindro. Este sólido es utilizado como una superficie Gausiana.
En geometría diferencial, un cilindro se define de forma general como cualquier superficie reglada generada por una familia uniparamétrica de líneas paralelas.
Esfera
En geometría, una superficie esférica es una superficie de revolución o el conjunto de los puntos del espacio cuyos puntos equidistan de otro interior llamado centro. Los puntos cuya distancia es menor que la longitud del radio forman el interior de la superficie esférica. La unión del interior y la superficie esférica se llama bola cerrada.
La esfera, como superficie de revolución, se genera haciendo girar una superficie semicircular alrededor de su diámetro.
Esfera proviene del término griego σφαῖρα, sphaîra, que significa pelota (para jugar). Coloquialmente hablando, se emplea la palabra bola, para describir al cuerpo delimitado por una esfera.
Solidos platonicos (Geometria)
Los sólidos platónicos o regulares son poliedros convexos cuyas caras son polígonos regulares iguales y en cuyos vértices se unen el mismo número de caras. Reciben este nombre en honor al filósofo griego Platón, a quien se atribuye haberlos estudiado en primera instancia. También se conocen como cuerpos platónicos, cuerpos cósmicos, sólidos pitagóricos, sólidos perfectos, poliedros de Platón o, con más precisión, poliedros regulares convexos.
Los sólidos platónicos son el tetraedro, el cubo (o hexaedro regular), el octaedro (o bipirámide cuadrada si se incluyera en la nomenclatura de sólidos de Johnson), el dodecaedro y el icosaedro (o bipirámide pentagonal giroelongada si se incluyera en la nomenclatura de sólidos de Johnson). Esta lista es exhaustiva, ya que es imposible construir otro sólido diferente de los cinco anteriores que cumpla todas las propiedades exigidas, es decir, convexidad y regularidad.
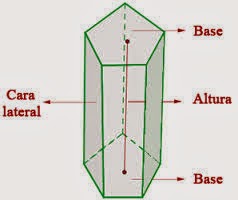
Prisma (Geometria)
Un prisma, en geometría, es un poliedro que consta de dos caras iguales y paralelas llamadas bases, y de caras laterales que son paralelogramos.
En el caso en que las caras laterales sean rectangulares, se llama prisma rectangular. El prisma rectangular o cuboides, y el prisma octagonal se encuentran entre los tipos de prisma recto, con una base rectangular y octagonal, respectivamente.
El volumen de un prisma recto es el producto del área de una de las bases por la distancia entre ellas (altura).
Piramide (Geometria)
Una pirámide es un poliedro limitado por una base, que es un polígono con una cara; y por caras, que son triángulos coincidentes en un punto denominado ápice.
El ápice o cúspide también es llamado vértice de la pirámide, aunque una pirámide tiene más vértices, tantos como el número de polígonos que lo limitan.
Cuerpos Geometricos
Un cuerpo geométrico es una figura geométrica tridimensional, es decir, que posee largo, ancho y alto, que ocupa un lugar en el espacio y que por lo tanto posee un volumen.
Los cuerpos geométricos se pueden clasificar a su vez en poliedros y cuerpos geométricos redondos o no poliedros.
Poliedros:
Los poliedros o cuerpos planos, son cuerpos geométricos cuyas caras son todas figuras geométricas exclusivamente planas. Entre los más conocidos se encuentran los siguientes:[]
Redondos:
Los cuerpos redondos son aquellos que tienen, al menos, una de sus caras o superficies de forma curva. Entre los más conocidos se encuentran:
Figuras geometricas
Una figura
geométrica es un conjunto no vacío cuyos elementos son puntos.[ ]Las
figuras geométricas son el objeto de estudio de la geometría, rama de las matemáticas
que se dedica a analizar las propiedades y medidas de las figuras en el espacio
o en el plano.
Para definir y
clasificar las figuras geométricas, comúnmente se debe recurrir a conceptos primitivos,
tales como el de punto, recta, plano y espacio, que en sí mismas también se
consideran figuras geométricas. A partir de ellas es posible obtener todas las
figuras geométricas, mediante transformaciones y desplazamientos de sus
componentes.[Ramas de la matematica
La Sociedad Estadounidense de
Matemática distingue unas 5000 ramas distintas de matemáticas.[] En una subdivisión amplia de
las matemáticas se distinguen cuatro objetos de estudio básicos: la cantidad,
la estructura, el espacio y el cambio que se corresponden a la aritmética, álgebra, geometría y cálculo. Además, hay ramas de las
matemáticas conectadas a otros campos como la lógica y teoría de conjuntos, y las matemáticas aplicadas.
Bomba Atomica
Una bomba atómica es un dispositivo que obtiene una gran cantidad de energía explosiva con reacciones nucleares. Su funcionamiento se basa en provocar una reacción nuclear en cadena descontrolada. Se encuentra entre las denominadas armas de destrucción masiva y su explosión produce una distintiva nube con forma de hongo. La bomba atómica fue desarrollada por Estados Unidos durante la Segunda Guerra Mundial gracias al Proyecto Manhattan, y es el único país que ha hecho uso de ella en combate (en 1945, contra las ciudades japonesas de Hiroshima y Nagasaki).
Su procedimiento se basa en la fisión de un núcleo pesado en elementos más ligeros mediante el bombardeo de neutrones que, al impactar en dicho material, provocan una reacción nuclear en cadena. Para que esto suceda hace falta usar núcleos fisibles o fisionables como el uranio-235 o el plutonio-239. Según el mecanismo y el material usado se conocen dos métodos distintos para generar una explosión nuclear: el de la bomba de uranio y el de la de plutonio.
En este caso, a una masa de uranio llamada subcrítica se le añade una cantidad del mismo elemento químico para conseguir una masa crítica que comienza a fisionar por sí misma. Al mismo tiempo se le añaden otros elementos que potencian (le dan más fuerza) la creación de neutrones libres que aceleran la reacción en cadena, provocando la destrucción de un área determinada por la onda de choque desencadenada por la liberación de neutrones.
Teorema de Pitagoras
El teorema de
Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
(el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los
cuadrados de los catetos (los dos lados menores del triángulo, los que
conforman el ángulo recto).
Hipotenusa 2 =
cateto 2 + cateto 2
c2
= a2 +
b2
martes, 28 de enero de 2014
Galileo Galilei
Galileo Galilei (Pisa, 15 de febrero de 1564 – Arcetri, 8 de enero de 1642) fue un astrónomo, filósofo, matemático y físico italiano que estuvo relacionado estrechamente con la revolución científica. Eminente hombre del Renacimiento, mostró interés por casi todas las ciencias y artes (música, literatura, pintura). Sus logros incluyen la mejora del telescopio, gran variedad de observaciones astronómicas, la primera ley del movimiento y un apoyo determinante para el copernicanismo. Ha sido considerado como el «padre de la astronomía moderna», el «padre de la física moderna» y el «padre de la ciencia».
Su trabajo experimental es considerado complementario a los escritos de Francis Bacon en el establecimiento del moderno método científico y su carrera científica es complementaria a la de Johannes Kepler. Su trabajo se considera una ruptura de las teorías asentadas de la física aristotélica y su enfrentamiento con la Inquisición romana de la Iglesia católica suele presentarse como el mejor ejemplo de conflicto entre religión y ciencia en la sociedad occidental.
Pitagoras
Pitágoras de Samos (569 a. C. - 475 a. C. ) fue un filósofo y matemático griego considerado el primer matemático puro. Contribuyó de manera significativa en el avance de la matemática helénica, la geometría y la aritmética, derivadas particularmente de las relaciones numéricas, y aplicadas por ejemplo a la teoría de pesos y medidas, a la teoría de la música o a la astronomía. Es el fundador de la Hermandad Pitagórica, una sociedad que, si bien era de naturaleza predominantemente religiosa, se interesaba también en medicina, cosmología, filosofía, ética y política, entre otras disciplinas. El pitagorismo formuló principios que influyeron tanto en Platón como en Aristóteles y, de manera más general, en el posterior desarrollo de la matemática y en la filosofía racional en Occidente.
No se ha conservado ningún escrito original de Pitágoras. Sus discípulos -los pitagóricos- invariablemente justificaban sus doctrinas citando la autoridad del maestro de forma indiscriminada, por lo que resulta difícil distinguir entre los hallazgos de Pitágoras y los de sus seguidores. Se le atribuye a Pitágoras la teoría de la significación funcional de los números en el mundo objetivo y en la música; otros descubrimientos, como la inconmensurabilidad del lado y la diagonal del cuadrado o el teorema de Pitágoras para los triángulos rectángulos, fueron probablemente desarrollados por la escuela pitagórica.
Albert Einstein
Albert Einstein fue un físico y judío alemán del siglo XIX y XX (Nació el 14 de marzo de 1879 y murió el 18 de abril de 1955) conocido principalmente por el desarrollo de la teoría de la relatividad (especial y general) y la explicación teórica del movimiento browniano y el efecto fotoelectronico.
Nació en la ciudad alemana de Ulm, pero al año de vida su familia se mudó a Munich, donde viviría hasta los 15 años. Con 17 ingresó en la Escuela Politécnica Federal de Zurich para estudiar matemáticas y física. Cinco años más tarde, ya graduado, consiguió la nacionalidad suiza y en 1902 comenzó a trabajar en la Oficina Federal de la Propiedad Intelectual de Suiza, empleo que compaginó hasta los 30 años con sus investigaciones científicas.
1905 fue su año más fructífero, resultado de la publicación de cuatro artículos científicos sobre el efecto fotoeléctrico, el movimiento browniano, la teoría de la relatividad especial y la equivalencia masa-energía (E = mc²). El primero le valió el Premio Nobel de Física del año 1921, el segundo el grado de doctor y los dos últimos le consagrarían, con el tiempo, como el mayor científico del siglo XX.
En 1908 comenzó a ejercer como profesor de física en la universidad de Berna, cargo que continuaría años posteriores en Praga y finalmente en Berlín, ciudad en la que vivió hasta que el ascenso del régimen nazi le hiciera abandonar Alemania y mudarse a Estados Unidos (1932). Allí impartió docencia en el Instituto de Estudios Avanzados de Princeton, se nacionalizó estadounidense (obteniendo la doble nacionalidad suizo-estadounidense) y pasó el resto de su vida intentando integrar las leyes físicas de la gravitación y el electromagnetismo así como divulgando valores pacifistas, socialistas y sionistas.
Charles Coulomb
Coulomb, Charles de (1736-1806), físico francés y pionero en la teoría
eléctrica;nació en Angulema y trabajó como
ingeniero militar al servicio de Francia en lasIndias Occidentales
(actuales Antillas), pero se retiró a Blois (Francia), en la épocade la
Revolución Francesa para continuar con sus investigaciones en
magnetismo,rozamiento y electricidad.En 1777
inventó la balanza de torsión para medir la fuerza de atracciónmagnética y eléctrica. Con este invento, Coulomb
pudo establecer el principio,conocido ahora como ley de Coulomb, que rige la
interacción entre las cargaseléctricas. En
1779 Coulomb publicó el tratado Teoría de las máquinas simples donde
seencuentra un análisis del rozamiento en la maquinaria. Después de la
Revolución,Coulomb salió de su retiro
y ayudó al nuevo gobierno en la planificación de unsistema métrico decimal de
pesos y medidas. La unidad de medida de cargaeléctrica, el culombio,
recibió este nombre en su honor.
Nicolas Copernico
Copérnico, Nicolás (1473-1543). Astrónomo polaco, conocido por su teoría
quesostenía que el Sol se encontraba en el centro del Universo y la Tierra, que
girabauna vez al día sobre su eje, completaba cada año una vuelta alrededor de
él: Teoríaheliocéntrica.Estudio humanidades, después derecho y medicina. En
Bolonia entró en contactocon el matemático
Domenico Maria de Novara, que criticó la exactitud de laGeografía de
Tolomeo (S.II). Este profesor fomentó el interés de Copérnico por lageografía y
la astronomía.En 1500, se doctoró en astronomía en Roma. Al año siguiente
estudió medicinaen Padua y sin haber acabado estos estudios, se licenció en
derecho canónico 1503y regresó a Polonia.Entre 1507 y 1515 escribió un tratado
breve de astronomía, Commentariolus (Dehypothesibus motuum coelestium a se
constitutis commentariolus), publicado en elS.XIX
y que sentó las bases de la concepción heliocéntrica de la astronomía: laTierra
giraba sobre sí misma una vez al día, y que una vez al año daba una
vueltacompleta alrededor del Sol.Aportó un
nuevo orden en alineación de los planetas según sus periodos derotación.
A diferencia de Tolomeo, vio que cuanto mayor era el radio de la órbita deun planeta, más tiempo tardaba en dar una vuelta
completa alrededor del Sol. Laidea de que la Tierra se movía era difícil de
aceptar en el S.XVI y aunque parte desu teoría fue admitida, la base
principal fue rechazada.Fue objeto de
numerosas críticas, en especial de la Iglesia, por negar que laTierra
fuera el centro del Universo. La mayoría de sus seguidores servían a la cortede
reyes, príncipes y emperadores. El más importante fue Galileo . Con
posterioridad a la supresión de la teoría de Copérnico, tras el juicioeclesiástico a Galileo en 1633, que lo condenó por
corroborar su teoría, algunosfilósofos jesuitas la siguieron en secreto.
En el siglo XVII, con el auge de las teoríasde
Isaac Newton sobre la fuerza de la gravedad, la mayoría de los pensadores enGran
Bretaña, Francia, Países Bajos y Dinamarca su teoría.
Georg Cantor
Cantor, Georg (1845-1918), matemático alemán,
nacido en San Petersburgo(Rusia). Dio clases en la Universidad de Halle, de
la que fue catedrático a partir de1872. Sus primeros trabajos con las series de
Fourier lo condujeron al desarrollo deuna teoría de los números irracionales.Cantor también formuló la teoría de conjuntos,
sobre la que se basa lamatemática moderna. Esta teoría extiende el
concepto de número al introducir losnúmeros
infinitos o, como él los denominaba, números transfinitos. La obra deCantor fue
responsable en gran medida de la posterior investigación crítica de losfundamentos
de las matemáticas y de la lógica matemática.
Arquimedes
Arquímedes (287-212 a.C.), matemático
e inventor griego, que escribióimportantes obras sobre la geometría plana y del
espacio, la aritmética y lamecánica.Nació en Siracusa y se educó en Alejandría. En el campo de las
matemáticaspuras, se anticipó a muchos de los descubrimientos de la ciencia
moderna, como elcálculo integral, con sus estudios de áreas y volúmenes de
figuras sólidas curvadasy de áreas de
figuras planas. Demostró también que el volumen de una esfera esdos
tercios del volumen del cilindro que la circunscribe.En mecánica, Arquímedes definió la ley de la palanca y se le reconoce
como elinventor de la polea
compuesta. También descubrió maquinaria de guerra:catapulta y un sistema de espejos que incendiaba
las embarcaciones enemigas alenfocarlas con los rayos del sol.Arquímedes es conocido sobre todo por el
descubrimiento de la ley de lahidrostática, conocida como el principio
de Arquímedes: "todo cuerpo sumergido enun fluido experimenta una pérdida
de peso igual al peso del volumen del fluido quedesaloja".
Aristoteles
Aristóteles (384-322 a.C.), filósofo y científico
griego, es uno de los filósofos más destacados
de la antigüedad. Escribió entre otros ensayos, un resumen de las doctrinas de Pitágoras; del que han sobrevivido
pocos extractos. Estos textos sebasan en gran parte en las anotaciones
recopiladas y ordenadas por sus editoresposteriores. Entre ellos están los tratados de lógica llamados Organon('instrumento'), ya que proporcionan los medios
con los que se ha de alcanzar elconocimiento positivo.En lógica,
desarrolló reglas para establecer un razonamiento encadenado que, sise respetaban y si la reflexión partía de premisas
verdaderas (reglas de validez ),no producirían falsas conclusiones ). En
el razonamiento, los nexos básicos eran lossilogismos:
proposiciones emparejadas que, en su conjunto, proporcionaban unanueva
conclusión. En el ejemplo más famoso, "Todos los humanos son
mortales" y"Todos los griegos son humanos", se llega a la
conclusión válida de que "Todos losgriegos son mortales".La ciencia es el resultado de construir sistemas
de razonamiento cada vez máscomplejos. Distinguía entre la dialéctica y
la analítica. La dialéctica sólo compruebalas opiniones por su consistencia
lógica. La analítica, trabaja de forma deductiva apartir de principios que
descansan sobre la experiencia y una observación precisa.Ello supone una ruptura con el pensamiento de
Platón, donde la dialéctica era elúnico
método lógico válido, tan eficaz para aplicarse en la ciencia como en lafilosofía.
Propiedades de las ecuaciones
1- Si ambos miembros de una ecuacion se le suma o resta la misma cantidad la igualdad se mantiene.
2- Si ambos miembros de una ecuacion se le multiplica o divide la misma cantidad la igualdad se mantiene.
3- Si ambos miembros de la ecuacion se elevan a un mismo numero o se extrae la raiz la igualdad se mantiene.
2- Si ambos miembros de una ecuacion se le multiplica o divide la misma cantidad la igualdad se mantiene.
3- Si ambos miembros de la ecuacion se elevan a un mismo numero o se extrae la raiz la igualdad se mantiene.
Ecuaciones
Es una igualdad entre dos expreciones algebraicas.
Las ecuaciones pueden ser:
a) Lineales o de primer grado
b) Cuadraticas o de segundo grado
c) Cubicas o de tercer grado
Segun el teorema fundamental del algebra una ecuacion tiene tantas soluciones como su mayor exponente.
Las ecuaciones pueden ser:
a) Lineales o de primer grado
b) Cuadraticas o de segundo grado
c) Cubicas o de tercer grado
Segun el teorema fundamental del algebra una ecuacion tiene tantas soluciones como su mayor exponente.
Pendiente de una recta
Es la inclinacion que tiene la recta. La pendiente se define como la variacion de Y entre la variacion de X.
M=y/x M=(y2-y1)/(x2-x1)
Si la recta es asendente (sube) la pendiente es positiva, y, si la recta es desendinte (baja) la pendiente es negativa.
M=y/x M=(y2-y1)/(x2-x1)
Si la recta es asendente (sube) la pendiente es positiva, y, si la recta es desendinte (baja) la pendiente es negativa.
lunes, 27 de enero de 2014
Producto cartesiano
Si A y B son conjuntos no vacios, su producto cartesiano, AxB, es el conjunto de pares ordenados (x,y) cuyos primeros componentes, x, son elementos del conjunto A y cuyos segundos componentes, y, son elementos del conjunto B.
Ej:
Si A={1,2} y B={1,3,5} su producto carteciano, AxB, es el siguiente conjunto de pares ordenados.
AxB={(1,1)(1,3)(1,5)(2,1)(2,3)(2,5)}
Ej:
Si A={1,2} y B={1,3,5} su producto carteciano, AxB, es el siguiente conjunto de pares ordenados.
AxB={(1,1)(1,3)(1,5)(2,1)(2,3)(2,5)}
Regla de Ruffini
Es un proceso para determinar el cociente y el residuo de las division de un polinomio P(x) por un binomio X+A. Este metodo fue inventado por Paolo Ruffini.
Ejemplo:
Ejemplo:
Composicion de las estructuras algebraicas
* Ley de componsicion interna. Es una operacion que asocia pareja de elementos X e Y de uun conjunto A a un conjunto Z del propio conjunto.
* Semigrupos. (Ley de composición interna, Asociativa)
* Monoide. ( Semigrupo, Existe neuto)
El elemento neutro es aquel elemento que operado con cualquien otro da como resultado ese otro elemento. En caso de una tabla el elemento neutro es aquel elemento donde se repite la primera columna. El elemento neutro de un compuesto es unico.
* Grupo. (Monoide, Existe en simetrico de cada elemento)
El elemento simetrico es aquel que operado con otro elemento me da el neutro.
* Grupo abeliano. (Grupo, Comutativa)
* Anillo. (Grupo abeliano, Semigrupo)
* Semigrupos. (Ley de composición interna, Asociativa)
* Monoide. ( Semigrupo, Existe neuto)
El elemento neutro es aquel elemento que operado con cualquien otro da como resultado ese otro elemento. En caso de una tabla el elemento neutro es aquel elemento donde se repite la primera columna. El elemento neutro de un compuesto es unico.
* Grupo. (Monoide, Existe en simetrico de cada elemento)
El elemento simetrico es aquel que operado con otro elemento me da el neutro.
* Grupo abeliano. (Grupo, Comutativa)
* Anillo. (Grupo abeliano, Semigrupo)
Estucturas algebraicas
Una estructura algebraica es un conjunto de elementos arbitrarios dotados de una o mas leyes de composicion interna.
Las estructuras algebraicas son utilizada para los programadores para la creacion de codigos que se entrelasan entre si. Los biologos para la interpretacion de las leyes de Mender sobre el crusamiento genetico.
Las estructuras algebraicas son utilizada para los programadores para la creacion de codigos que se entrelasan entre si. Los biologos para la interpretacion de las leyes de Mender sobre el crusamiento genetico.
La matematicas
Las matemáticas, es una ciencia formal que, partiendo de axiomas
y siguiendo el razonamiento lógico, estudia las propiedades y relaciones entre
entidades abstractas con numeros, figuras geometricas o simbolos , pese a que también es discutido su carácter
científico.
Las matematicas forman una ciencia que an evolucionado en el tiempo, simbologia, procedimiento e interpretacion. De todos los lenguajes que existen el de las matematicas es el mas util porque con el se a interpretado lo que sucede en la naturalesa, esas expreciones logicas compuestas por simbolos y numeros an sido los responsables de desarrollo de la tecnologia. Las ciencias naturales son las mas beneficiadas, las ciencias sociales emplean las matematicas para realizar sus investigaciones cuantitativas.
domingo, 26 de enero de 2014
La geometria
La geometria: es una rama de la matematica que se ocupa del estudio de las propiedades de las figuras en el plano o el espacio.
Es una de las ciencias mas antiguas. Inicialmente constituida en un cuerpo de conocimientos practicos en relacion con las longitudes, ares y volumenes. Sus origenes se remontan a la solucion de problemas concretos relativos a medidas.
Conceptos no definidos de la geometria:
* Puntos: carese de dimension, no tiene longitud, anchura, ni espesor. (Es lo mas pequeño que se encuentra).
* Linea: posee una sola longitud. (Es la union sucesiva de puntos).
A<---------------->B
* Plano: se encuentran infinitos puntos, tiene dos longitudes, largo y ancho.
Es una de las ciencias mas antiguas. Inicialmente constituida en un cuerpo de conocimientos practicos en relacion con las longitudes, ares y volumenes. Sus origenes se remontan a la solucion de problemas concretos relativos a medidas.
Conceptos no definidos de la geometria:
* Puntos: carese de dimension, no tiene longitud, anchura, ni espesor. (Es lo mas pequeño que se encuentra).
* Linea: posee una sola longitud. (Es la union sucesiva de puntos).
A<---------------->B
* Plano: se encuentran infinitos puntos, tiene dos longitudes, largo y ancho.
Suma de los angulos interiores
Para determinar la sumatoria de los angulos interiores se utiliza la expresio:
S=(n-2) 180
S=(n-2) 180
Nombres de los poligonos, segun sus lados
Triangulo= 3 lados
Cuadrados= 4 lados
Pentagono= 5 lados
Hexagono= 6 lados
Heptagono= 7 lados
Octagono= 8 lados
Nonagono= 9 lados
Decagono= 10 lados
Endecagono= 11 lados
Dodecagano= 12 lados
Total de diagonales a un poligono
Para encontrar el total de diagonales de un poligono se utiliza la exprecion:
D=n(n-3)
2
Donde (n) es el numero de lados del poligono
Diagonales de un vertice
Para encontra diagonales desde un vertice se utiliza la exprecion:
d=n-3
Donde (n) es el numero de lados del poligono
Diagonales de un poligono.
Una diagonal
Una diagonal es un segmento de recta que une dos vertices no consecutivos.
Una diagonal es un segmento de recta que une dos vertices no consecutivos.
Poligono circunscrito.
Poligono circunscrito
Un poligono circunscrito a una circunferencia tiene sus lados tangentes a dicha circunferencia.
Un poligono circunscrito a una circunferencia tiene sus lados tangentes a dicha circunferencia.
Poligonos inscritos.
Poligonos inscritos
Un poligono esta inscrito en una circunferencia si todos sus vertices pertenecen a la circunferencia
Un poligono esta inscrito en una circunferencia si todos sus vertices pertenecen a la circunferencia
Angulos internos y externos de un poligono regular
Angulos internos
La medida, M, de los angulos internos de un poligono regular se calcula con:
|
M=180(n- 2)
|
|
n
|
Angulos externos
La medida, M, de los angulos externos de un poligono regular se obtiene con:
|
M=360
|
|
n
|
jueves, 23 de enero de 2014
Polígonos convexos y cóncavos
Polígono convexo:

Un polígono convexo es una figura en la que todos los ángulos interiores miden menos de 180 grados o  radianes y todas sus diagonales son interiores.Cualquier recta que pase por un lado de un polígono convexo deja a todo el polígono completamente en uno de los semiplanos definidos por la recta.Un polígono es convexo solo si cualquier segmento entre dos puntos que estén dentro del mismo está dentro, es decir, el segmento no corta los lados.
radianes y todas sus diagonales son interiores.Cualquier recta que pase por un lado de un polígono convexo deja a todo el polígono completamente en uno de los semiplanos definidos por la recta.Un polígono es convexo solo si cualquier segmento entre dos puntos que estén dentro del mismo está dentro, es decir, el segmento no corta los lados.
Polígono cóncavo:
Los "polígonos cóncavos" son aquellas figuras en las que al menos uno de sus ángulos interiores mide más de 180 grados ó  radianes. En un polígono cóncavo al menos una de sus diagonales es exterior al polígono. Los polígono estrellado son polígonos cóncavos. En todo polígono cóncavo hay al menos dos vértices que al ser unidos por un segmento, este corta uno o más lados. Los polígonos de tres lados (triángulos) son los únicos polígonos que no pueden ser cóncavos, dado que ninguno de sus tres ángulos puede superar los 180 grados ó
radianes. En un polígono cóncavo al menos una de sus diagonales es exterior al polígono. Los polígono estrellado son polígonos cóncavos. En todo polígono cóncavo hay al menos dos vértices que al ser unidos por un segmento, este corta uno o más lados. Los polígonos de tres lados (triángulos) son los únicos polígonos que no pueden ser cóncavos, dado que ninguno de sus tres ángulos puede superar los 180 grados ó  radianes
radianes
Suscribirse a:
Comentarios (Atom)